標準偏差と製造原価の関係

今回は標準偏差について解説していきます。基本的な用語解説から、ばらつきを改善すると原価を改善できるかもしれないというお話までさせていただきます。

Genkanのデータアナリストとして工場の原価分析を行っています吉田充慧と申します。よろしくお願いいたします。

標準偏差は分散の平方根で求めることができます。分散はデータのばらつきを表し各データとそのデータの平均の差の二乗和をデータ数で割ることで求めることができます。分散だと式の性質上、単位が二乗されたものが算出されます。そこで平方根をとって標準偏差を求めることで元のデータと同じ単位が扱えます。

標準偏差や分散はデータの分散度あるいは、ばらつきを表すいろいろな尺度の中で最も良く用いられる代表的な値です。

これらの値は統計学的な検定などにも用いられる非常に重要な尺度です。

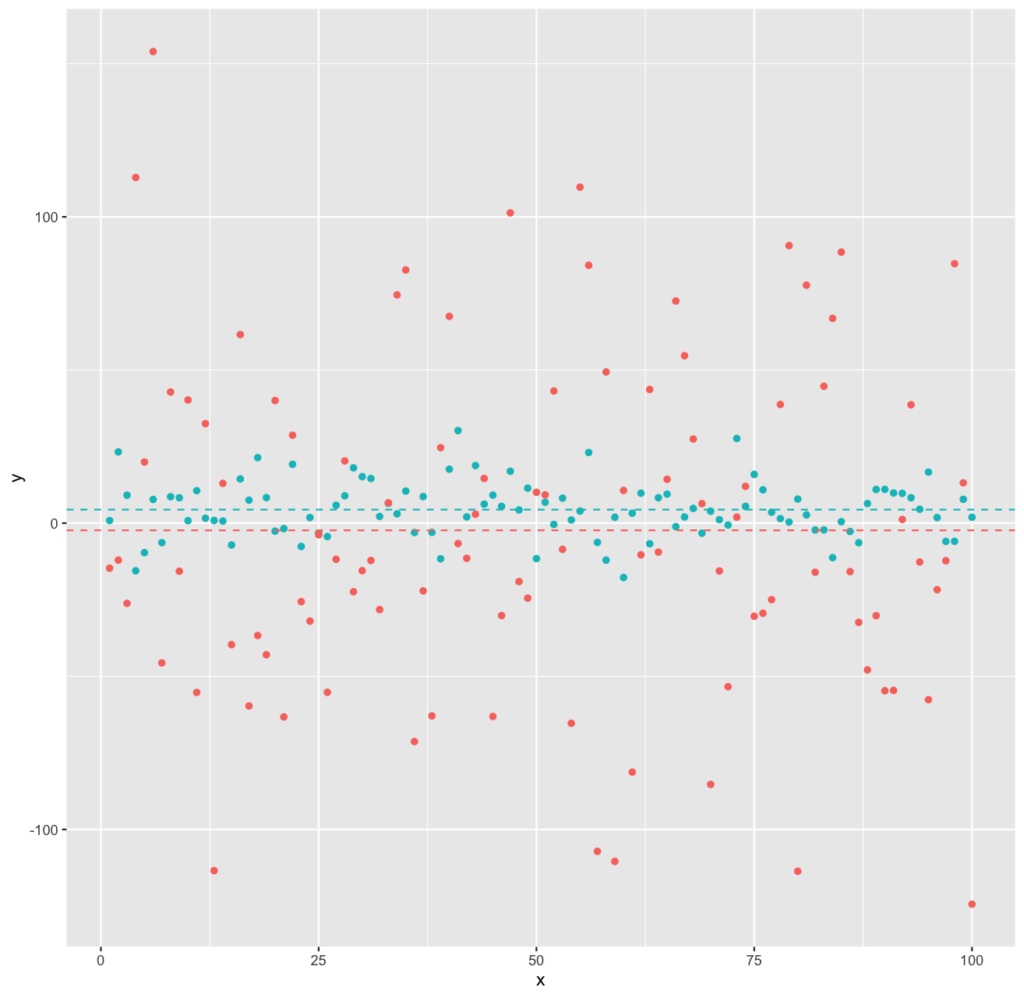
具体的にばらつきがあるとはどういうことか。以下に標準偏差の異なる二つの散布図を用意しました。

青いプロットの標準偏差はおよそ10　赤いプロットの標準偏差はおよそ50
点線は各データの平均値を示しています。

実際にこれをサイクルタイムの散布図として考えてみると、原価の効率が良いのは平均サイクルタイムの早い赤いプロットのデータになります。
つまり、実際原価は平均サイクルタイムを考慮するので標準偏差の大小は関係ありません。

標準偏差は実際原価には関係ありませんが、見積もり原価に関わる可能性があります。例えば、ばらつき（標準偏差）の大きい工程を想定してみてください。

この工程の見積もり原価を計算する際にサイクルタイムをストップウォッチを使って計測する際、各データが大きく乖離しているとどの値を代表値にとるかを選ぶのは困難です。

また、10回ほど測定したサンプルデータの平均値を見積もりに使用する場合、その平均値の信頼度はかなり低くなります。ばらつきがあるのに測定したサンプルが大小どちらかに偏ってしまうと見積もり原価を大きく外すことがあるのです。

サンプル数を増やすことでこの問題は解消できますが、ストップウォッチの計測にはデータの限りがあるでしょう。

標準偏差を算出するには、他にも重要なことがあります。それは標準偏差が大きい工程は原価を改善できる可能性があるということです。

これには前提として標準偏差を計算できるための十分なサンプルが必要です。

標準偏差が大きいと原価の改善可能性があるというのは、先述の散布図をみるとわかります。

ばらつきの少ない青いプロットでは作業が最適化されているので安定した作業を繰り返していることがわかります。このような作業ではこれ以上平均サイクルタイムを縮めることは難しいことが想定されます。

反対に、ばらつきの大きい赤いプロットでは作業者によってサイクルタイムが違ったり、作業が最適化されていない可能性を示します。また大きいサイクルタイムをなるべく散布の中心に集めることで大幅に平均サイクルタイムを改善することにつながります。

以上になります。ご質問、ご要望ありましたらお気軽にコメントやお問い合わせいただければ幸いです。

また、引き続き原価と統計の関係について更新していきますので、是非Genkanメールマガジンにご登録ください。

よろしくお願いいたします。